Recently I became very excited about functional programming and this post summarizes the first step of this journey.
During my master’s studies in Linz I had two courses dealing with functional programming: Once I learned Hashkell, but it was only a part of a general programming languages course and I also toke an “Object-functional Programming” course and learned a little bit of Scala.
Now I decided to learn OCaml, because it has a cool name is an ML language and from there I still can go to multiple directions like F# or even Scala again (but I think the other way around would be a little bit harder, since F# and Scala have more support for traditional imperative programming, and with OCaml I’m forced to write more functional style code).
Bte here are two career changing presentations:
Ok, so let’s start with the first program.
1. Sum with a higher order function
What it does:
It adds the two number, but only takes the one(s) where the test function returns true.
This is btw. an example for a higher order function: these are function which have a function in their parameter list and/or as their return types.
It takes three parameters:
- A function which takes a parameter and returns a Boolean.
let sum test first second = (if test first then first else 0)
+ (if test second then second else 0) ;;
The ;; at the end is basically the termination of this declaration (like ; in C/C++/C#, Java, etc.).
If you type this method into the top-level it also shows its type:
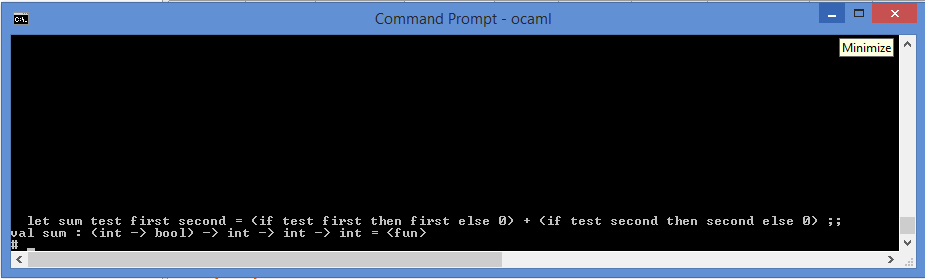
And here is the this function in anction:
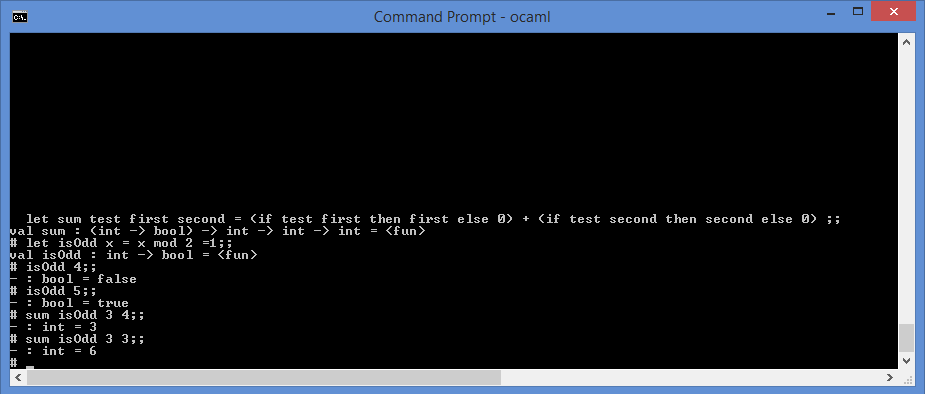
2. Recursive functions + pattern matching: Summing the items in an integer-list
In this example there are two typical functional programming constructs:
1) A recursive function is a function which calls itself, which also exists in non-functional languages, but here this concept seems to be used everywhere. There is a base case (which causes the recursion to terminate) and a case which makes sure that the execution moves forward.
Here the function takes 1 parameter, which is an integer-list and returns a number which is the sum of the elements in the list.
let rec sum list = match list with
| [] -> 0
| hd :: tail -> hd + ( sum tail ) ;;
2) Pattern matching is a similar concept to the switch-case statement with some powerful additions. For example in OCaml it should be exhaustive, if there is one case which you do not handle it gives you a warning (it’s better to convert this warning to a compiler error).
The rec keyword in the function declaration tells the compiler that the function is recursive (withut that you get a compilation error). The other new thing is this "match .. with" and the | signs. This is pattern matching and in this case it means that for an empty list it returns 0 (this is the base case) and for a non-empty list it gets the first element (hd) and sums the returned value from the sum function where it passes the rest of the list as the parameter (this steps ensures that the execution moves forward)
To see in in action:
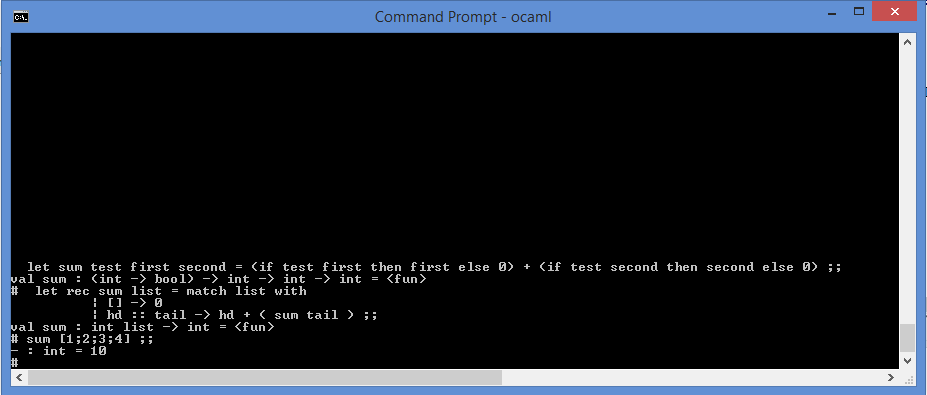
3. Merge sort
Tbc.
let rec mergeSortedLists l1 l2 = match l1, l2 with
| [], [] -> []
| [], l | l, [] -> l
| lhd::ltail, rhd::rtail
-> if lhd > rhd then
rhd :: mergeSortedLists (lhd::ltail) (rtail)
else
lhd :: mergeSortedLists ltail (rhd::rtail);;